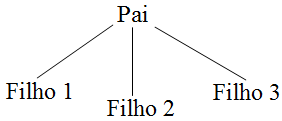
Árvores

Árvores

Definição: É uma estrutura onde a relação entre seus elementos é de um para vários, também denominada estrutura hierárquica.

Uma árvore consiste em um conjunto de nós, tal que:

Existe um nó denominado raiz.
Os demais nós formam m (m >= 0) conjuntos onde cada um deles também é uma árvore.

Notações gráficas para representar árvores:

Aplicações de Árvores

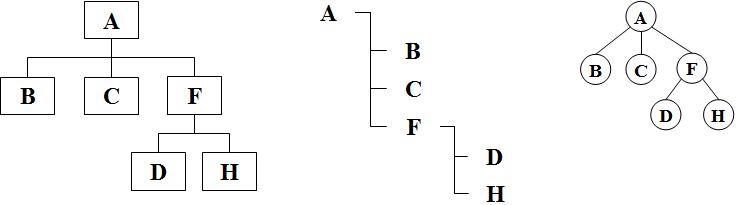
Árvores podem ser usadas em diversos tipos de aplicações:

Aplicações onde é necessário recuperar informações rapidamente (SGBD)
Programas onde as informações têm que ser estruturadas de forma hierárquica.
Aplicações onde é necessário armazenar expressões matemáticas.

Para representar as expressões matemáticas A + B * 3 e (A + B) * 3 poderíamos usar as árvores A e B abaixo:

Terminologia

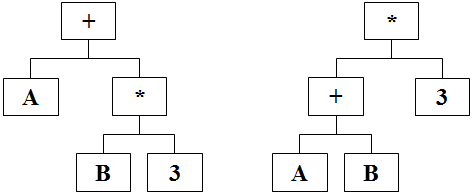
Cada elemento de uma árvore pode ser classificado como:

Classificação	Descrição
Pai	quando fica imediatamente acima de outro nó.
Filho	quando fica imediatamente abaixo de outro nó.
Irmãos	se os nós têm o mesmo pai.
Raiz	se não tem nó pai (pode ter filhos)
Folha ou Terminal	quando não possui filhos (pode ter pai)

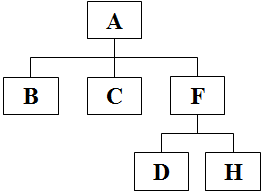
Dada a árvore acima, temos:

A, B, C, D, F e H são nós;
A é pai de B, C e F. F é pai de D e H;
B, C e F são filhos de A. D e H são filhos de F;
B, C e F são irmãos. D e H são irmãos;
A é a raiz da árvores;
B, C, D e H são folhas.

Ancestral: A é ancestral de B, C, F, D e H.

Descendente: B, C, F, D e H são descendentes de A. D e H são descendentes de F.

Arestas: são as ligações entre os nós.

Caminho: é uma seqüência de nós n₁, n₂, ... , n_i tal que os nós sejam distintos e que exista uma aresta entre cada par de nós.

Comprimento de um caminho: número de arestas que um caminho contém. Ex: A - F - D tem comprimento 2.

Nível de um nó: comprimento de um caminho que vai da raiz até o nó, sendo o nível do no raiz igual a 0. Ex: A tem nivel 0; B nível 1 e D nivel 2.

Altura de uma árvore: é o nível mais alto de uma árvore. A árvore do exemplo tem altura 2.

Grau de um nó: quantidade de subárvores de um nó. Ex: a tem grau 3, F tem grau 2 e B tem grau 0.

Grau da árvore: quantidade máxima de subárvores para cada nó da árvore.

Subárvore: é uma árvore formada por um dos nós filhos e seus descendentes.

Árvore Ordenada: árvore onde a ordenação de suas subárvores é importante.

Implementação Seqüencial

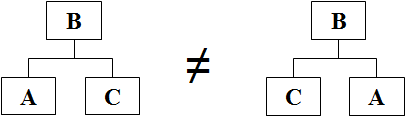
Na implementação seqüencial os nós de uma árvore são colocados seqüencialmente na memória. Há, basicamente, duas formas de implementação seqüencial de árvores. Uma para ser usada quando o grau da árvore é conhecido e outra quando é desconhecido.

Seja a árvore de exemplo abaixo:

A implementação com grau de árvore conhecido (no caso 3) seria:

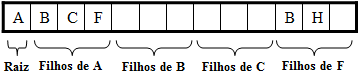
A implementação com grau de árvore desconhecido seria:

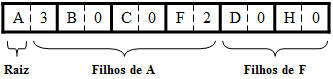
Desvantagens da implementação com grau de árvore conhecido:

Existe desperdício de espaço quando há nós com menos subárvores que o grau da árvore.
É necessário conhecer a altura da árvore antes de criar a estrutura.

Desvantagens da implementação com grau de árvore desconhecido:

Há desperdício de espaço devido ao indicador de grau do nó.
É necessário mais processamento para manipulações dos nós. Inserções e remoções provocam movimentações dos nós.

Implementação Encadeada

A implementação encadeada oferece:

Melhor aproveitamento de memória.
Chance de alterar dinamicamente o tamanho da árvore.

Há basicamente 2 formas de implementação encadeada:

Com grau conhecido (no caso 3)

Com grau da árvore desconhecido
- Cada nó da árvore contém:
  - Os dados
  - Uma lista encadeada com apontadores para n filhos (n >= 0)

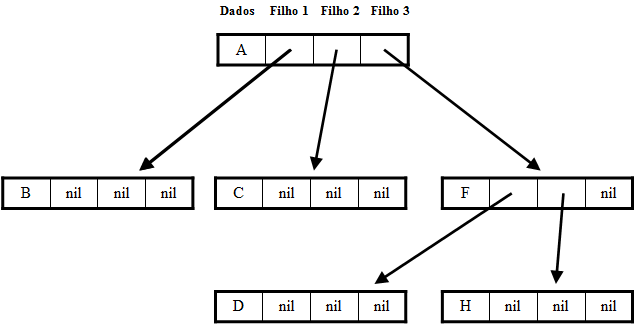
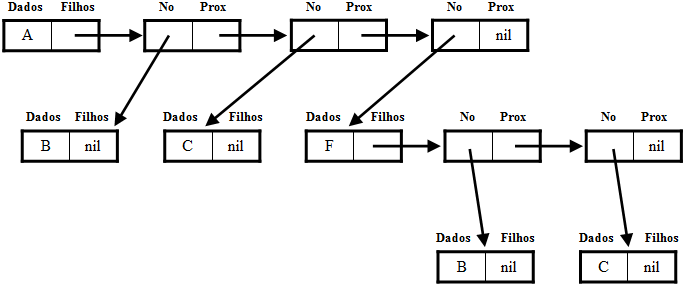
A implementação com grau de árvore conhecido é mais simples quando comparada à implementação com grau de árvore desconhecido.