Complexidade de Algoritmos

Complexidade de Algoritmos

Um algoritmo é um conjunto definido de instruções a serem executadas para resolver um problema.

Considerando as diversas soluções algorítmicas para um dado problema, como identificar a melhor? E melhor sob qual perspectiva? Podemos, a depender do objetivo, considerar critérios de análise de um algoritmo como: tempo, espaço, tamanho do código, eficácia, legibilidade, precisão e outros.

Avaliar a complexidade de uma algoritmo constitui-se em determinar os recursos exigidos (tempo, espaço, etc.):

Prever o crescimento dos recursos exigidos por um algoritmo à medida que o tamanho dos dados de entrada cresce.
Comparando os recursos exigidos por diferentes algoritmos que resolvem o mesmo problema (um algoritmo mais eficiente exige menos recursos para resolver o mesmo problema).

Métodos de Análise de Algoritmos

Podemos calcular/estimar o tempo de processamento de um algoritmo através de 2 métodos:

Empírico (experimental): efetuado a partir de testes de implementação do algoritmo.
Analítico (teórico): parte-se do pressuposto de que toda e qualquer instrução componente do algoritmo é executada em tempo constante e busca-se definir uma função t = f(n) onde t é o total de tempo de processamento e n é o tamanho da entrada. Vale ainda considerar que é usual ignorar o custo de algumas instruções e considerar apenas as mais significativas.

Qual método usar? O empírico tem como vantagem o fato de considerar condições reais. Já o analítico conta com a garantia da neutralidade em relação aos efeitos do tradutor e do hardware que podem mascarar a eficiência do algoritmo em análise. Assim, normalmente usamos o teórico.

Pelo método analítico, partimos do pressuposto de que toda e qualquer instrução contida no algoritmo é executada em tempo constante e buscamos definir uma função t = f(n), onde t é o total de tempo de processamento e n é o tamanho da entrada. Vale salientar que é usual ignorarmos o custo de algumas instruções e considerar apenas as mais significativas.

Exemplo 1: Cálculo da complexidade de um algoritmo que soma N números dados

Instruções	Custo
readln(N);	1
Cont:=1;	1
Soma:=0;	1
while Cont<=N do begin readln(Num); Soma:=Soma+Num; inc(Cont); end;	3n
Total	3 + 3n

Exemplo 2: Cálculo da complexidade de um algoritmo que calcula o somatório da série geométrica: 1 + x¹+ x²+ x³+ ... + xⁿ

Instruções	Custo
readln(X);	1
readln(N);	1
Soma:=0;	1
I:=0;	1
while I<=N do begin Produto:=1; J:=0; while J<I do begin Produto:=Produto*X; inc(J); end; Soma:=Soma + Produto inc(I); end;	(N² + N) / 2
Total	(N² + N) / 2 + 4

Para chegar à quantidade de vezes que o laço while mais interno é executado, podemos perceber que para qualquer valor de N, ele é executado um número de vezes igual ao somatório de uma progressão aritmétrica cujo termo inicial é 0, a razão é 1 e último termo é N.

Considerando que o valor de N informado é igual a 5, teríamos:

Quando I é igual a	While mais interno é executado
0	0
1	1
2	2
3	3
4	4
5	5

Considerando que o somatório de uma PA é calculado através da fórmula S = n * (u₁ + u_n) / 2, para N = 5, teríamos o somatório igual a 15.

Já que u₁ = 0 e u_n= N, podemos chegar à fórmula abaixo:

S = n * (u₁ + u_n) / 2
S = (N + 1) * (0 + N) / 2
S = (N + 1) * N / 2
S = (N² + N) / 2

Uma outra implementação possível para o cálculo é mostrada abaixo:

Instruções	Custo
readln(X);	1
readln(N);	1
Soma:=0;	1
I:=0;	1
while I<=N do begin Soma:=Soma*X+1; inc(I); end;	*2 N**
Total	*2 N + 4**

Comparando esta implementação com anteriormente mostrada, pode-se perceber que esta é bem mais eficiente.

Cálculo de Complexidade

Para simplificar o cálculo de complexidade algorítmica, fazemos algumas simplificações:

Consideramos que as entradas tendem ao infinito, pois para valores suficientemente pequenos de n, qualquer algoritmo custa pouco para ser executado, mesmo os ineficientes.
Destacamos o termo de mais alta ordem matemática já que como a entrada tende ao infinito, este termo é o que define o custo de execução de um algoritmo.
Ignoramos as constantes do termo destacado, já que apresentam peso insignificante ao considerar que n tende ao infinito.

Desta forma surge a notação O:

Complexidade	Notação O
2n + 2	O(n)
(n² + n)/2	O(n²)
log n + 4	O(log n)

Com base nestas regras, usamos algumas denominações de acordo com a complexidade ordem (O):

Ordens
O(k), sendo k constante	constante
O(log n)	logarítmica
O(n)	linear
O(n²)	quadrática
O(n³)	cúbica
Kⁿ	exponencial

As ordens estão dispostas na tabela acima em ordem crescente de complexidade, isto é, a de menor complexidade é a constante e a de maior complexidade é a exponencial.

Na tabela abaixo simulamos possíveis valores para n e verificamos como se comportam as Ordens de complexidade apresentadas:

n	O(log n)	O(n)	O(n²)	O(n³)
1	0,00	1	1	1
2	1,00	2	4	8
3	1,58	3	9	27
4	2,00	4	16	64
5	2,32	5	25	125
6	2,58	6	36	216
7	2,81	7	49	343
8	3,00	8	64	512
9	3,17	9	81	729
10	3,32	10	100	1000

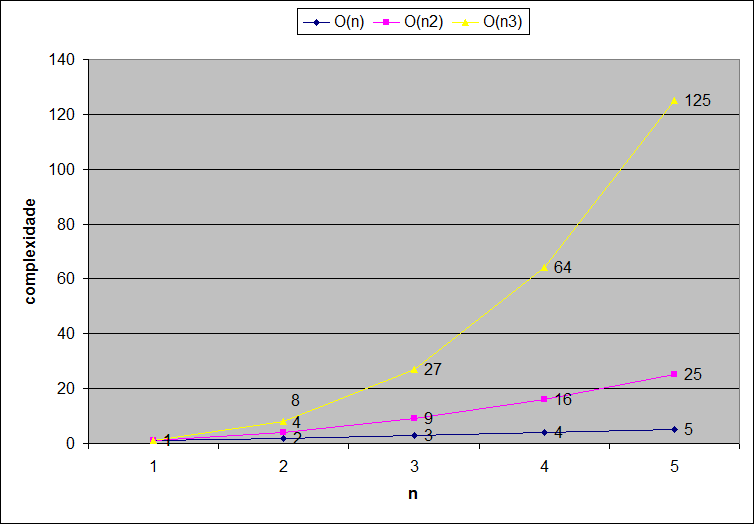
Graficamente, podemos visualizar melhor como a complexidade de uma função cúbica aumenta muito mais do que uma linear ou quadrática:

Melhor caso, Pior caso e caso Médio

Há algoritmos em que o custo (tempo de execução), não é uniforme para as entradas de tamanho n.

Por exemplo, no caso do algoritmo que determina o maior elemento de um vetor de inteiros:

A complexidade é O(n), caso seja usado um vetor desordenado, já que todos os elementos devem ser analisados e só é necessário fazer uma passagem pelo vetor.
Já em um vetor ordenado, a complexidade seria O(k), já que bastaria acessar o último valor do vetor.

Em outras palavras, a forma como os dados de entrada encontram-se dispostos, exerce influência no comportamento de alguns algoritmos tornando o cálculo de complexidade não exato.

Assim, ao apresentarmos o cálculo de complexidade de algoritmos, devemos esclarecer se este refere-se ao melhor caso, ao caso médio ou ao pior caso de arranjo de entrada, onde:

O de melhor caso corresponde ao de menor tempo de execução sobre todos os possíveis arranjos de entradas de tamanho n.
O de pior caso corresponde ao de maior tempo de execução sobre todos os possíveis arranjos de entrada de tamanho n.
O caso médio, ou caso esperado, corresponde à média dos tempos de execução de todas as entradas de tamanho n. É o mais difícil de ser obtido por depender de distribuições de probabilidade.

O cálculo de complexidade de soluções algorítmicas não é só aplicado para identificação da melhor solução dentre diversas, mas também para predizer o comportamento não exato, relativo ao tempo de execução de um algoritmo, independente de sua implementação efetiva.