Classificação
Conceito: Classificar dados é o processo pelo qual se determina a ordem em que devem ser apresentados os dados, geralmente em forma de tabela, de modo que obedeçam a seqüência estabelecida por um ou mais de seus campos. Estes campos especificados como determinantes da ordem de classificação são chamados de chaves de classificação.
Ambiente de classificação: As características do meio no qual estão armazenados os dados afetam de forma decisiva o processo de classificação, uma vez que existem diferenças acentuadas no modo como os dados são acessados na memória principal e na memória secundária.
Dessa forma, os métodos de classificação de dados contidos inteiramente na memória principal (classificação interna) podem envolver a manipulação em qualquer seqüência, ao passo que os métodos de classificação de dados armazenados em memória secundária (classificação externa), bloco a bloco.
O resultado de um processo de classificação é a seqüência ordenada das entradas que se deseja classificar. Várias são as alternativas que podemos especificar a ordem na qual devem ser apresentados os dados classificados. As mais comuns são:
Nesta alternativa as entradas são remanejadas fisicamente de modo que no final da classificação estarão fisicamente ordenadas na seqüência especificada pela chave de classificação.
Esta alternativa, muitas vezes, pode gerar um custo bastante alto, uma vez que, envolve a movimentação física das entradas da tabela para suas novas posições. Por exemplo, para a tabela abaixo (desordenada), onde só é mostrada a chave de classificação, teríamos como resultado a tabela abaixo da original (ordenada).
Tabela original (desordenada):
| Endereço Físico | Chave | Dados |
|---|---|---|
| 1 | 10 | DCOMP |
| 2 | 50 | DFI |
| 3 | 20 | DEC |
| 4 | 30 | DEL |
| 5 | 90 | DEQ |
Tabela modificada (ordenada):
| Endereço Físico | Chave | Dados |
|---|---|---|
| 1 | 10 | DCOMP |
| 2 | 20 | DEC |
| 3 | 30 | DEL |
| 4 | 50 | DFI |
| 5 | 90 | DEQ |
Nesta alternativa as entradas são mantidas nas suas posições originais e a seqüência de ordenação é ditada por meio de um vetor que é gerado durante o processo de classificação. Usando os mesmos dados do exemplo anterior teríamos a tabela de entradas e um vetor indireto de ordenação associado, como é mostrado abaixo.
| Endereço Físico | Chave | Dados |
|---|---|---|
| 1 | 10 | DCOMP |
| 2 | 50 | DFI |
| 3 | 20 | DEC |
| 4 | 30 | DEL |
| 5 | 90 | DEQ |
Vetor indireto de ordenação:
| Endereço Físico | Ordem |
|---|---|
| 1 | 1 |
| 2 | 3 |
| 3 | 4 |
| 4 | 2 |
| 5 | 5 |
A vantagem principal desta alternativa é que ela não envolve a movimentação das entradas da tabela e suas posições originais. Note que é possível classificarmos uma mesma tabela segurando diversos critérios diferentes, obtendo conseqüentemente um vetor indireto de ordenação para cada uma das chaves.
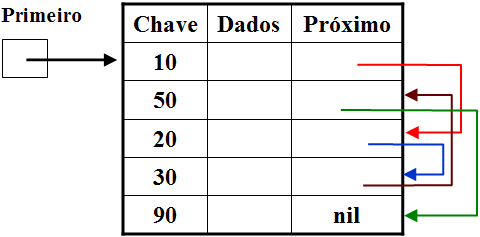
Nesta alternativa, as entradas são mantidas nas suas posições originais e uma lista encadeada que inclui todas as entradas da tabela ordenadas pelo valor da chave, é gerada durante o processo de classificação.
Diferentemente da alternativa anterior, onde o vetor indireto de ordenação é separado da tabela de dados, nesta alternativa um campo é acrescido à tabela para indicar a seqüência ordenada. Em cada entrada, o conteúdo do campo é igual ao endereço da próxima entrada na ordem de classificação.
Esta alternativa permite também a ordenação de uma mesma tabela segundo diferentes critérios, através do uso de campos adicionais para o encadeamento.

Os métodos de classificação estão agrupados em várias famílias. Dentre elas temos:
Definição: A característica comum a todos os métodos de classificação por inserção é que eles efetuam a ordenação da lista pela inserção de cada um dos elementos em sua posição correta dentro de uma sublista classificada.
Método de Inserção Direta
Neste método os elementos da lista são divididos em dois segmentos. Inicialmente, o primeiro segmento contém apenas o 1º elemento (a1) estando portanto classificado. O segundo segmento, formado pelos elementos a2, a3, ..., an (sendo n o número de elementos da lista) continua sem ordenação.
Por meio de iterações sucessivas, cada elemento do 2º segmento é inserido ordenadamente no 1º, até que todos sejam inseridos. O funcionamento do método é mostrado abaixo.
Lista Original: 10, 50, 20, 30 e 90
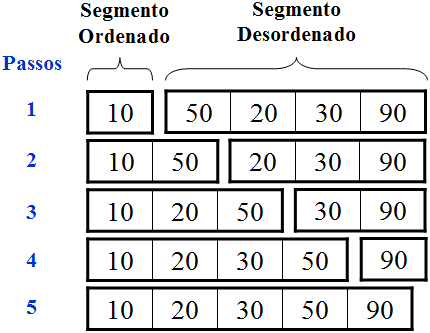
Para ver a implementação do método de inserção direta, abra as units DefDados e Insercao.
Definição: Caracteriza-se por efetuar a classificação através da comparação sucessiva de pares de elementos, trocando de posição caso esteja fora da ordem desejada.
Método da Bolha
A cada passo, cada elemento da lista é comparado com o seu sucessor, sendo os dois trocados de posição caso estejam fora de ordem. São executados tantos passos quanto necessários, até que em um deles não ocorram trocas, estando assim a lista ordenada.
Em cada passo, o valor é borbulhado para a última posição do segmento da lista considerada.
No 1º passo, o segmento tem o tamanho da lista, e nos passos seguintes o seu tamanho é determinado pela posição onde ocorreu a última troca. O funcionamento do método é mostrado abaixo.
Lista Original: 50, 40, 30, 20 e 10
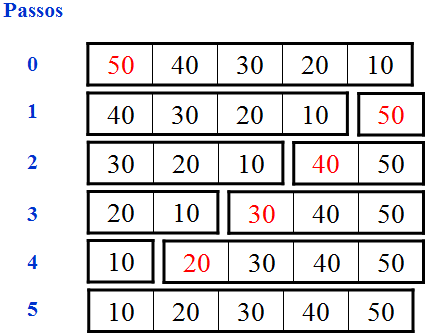
Para ver a implementação do método da Bolha, abra a unit Troca.
Método Quick Sort
Este método baseia-se no princípio de que é mais rápido classificar duas listas de N/2 elementos do que apenas uma com N elementos, ou seja, aplica o princípio "dividir para conquistar".
A partição começa através da seleção de um elemento da lista. O elemento escolhido é chamado pivô. Há vários critérios para escolhê-lo, mas adotaremos o elemento central (que normalmente é uma boa escolha).
O particionamento é obtido tomando o elemento pivô e, por comparações e troca sucessivas, fazendo com que os menores valores ou iguais ao pivô passam para a esquerda e os maiores para sua direita.
Para executar uma determinada partição foram introduzidos dois apontadores (indicadores): o primeiro (I) começa na posição 1 do segmento e percorre para a direita; o segundo (J) começa no final do segmento e o percorre para a esquerda. O apontador (I) procura elementos maiores que o pivô e o apontador (J) por elementos menores ou iguais ao pivô. O processo termina quando o apontador (I) é maior ou igual ao apontador (J).
Lista Original: 50, 40, 30, 20 e 10
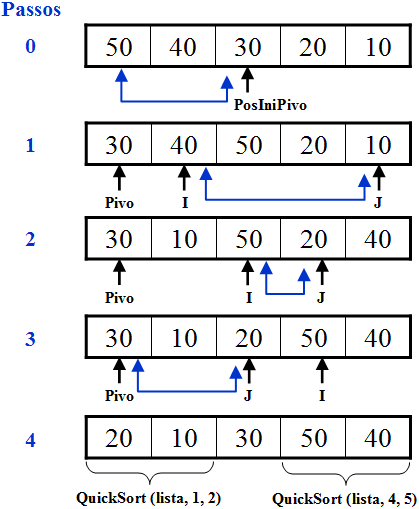
Para ver a implementação do método Quick Sort, abra a unit Troca.
Definição: Nos métodos de classificação por seleção a ordenação é efetuada pela seleção sucessiva do menor valor da lista. A cada passo o elemento de menor valor é colocado em sua posição definitiva na lista classificada e o processo é repetido para o segmento que contém os elementos não selecionados.
Método de Seleção Direta
Este método consiste em se determinar a posição do menor valor dentre N elementos a1, a2, ..., an é trocar o elemento que está nessa posição como que está na posição 1. Em seguida, determina-se a posição do menor elemento de a2 até an e troca-se o elemento que está nessa posição com o que está na posição. O processo continua até que o menor valor entre an-1 e an é trocado (se necessário) e colocado na posição n-1.
Lista Original: 10, 50, 20, 30 e 90

Para ver a implementação do método de Seleção Direta, abra a unit Selecao.
Definição: Nos métodos de classificação por intercalação a ordenação é efetuada pela divisão da lista não ordenada em listas menores, que são ordenadas separadamente e depois unidas de forma que seus elementos sejam intercalados em uma lista ordenada. Desta forma, a cada intercalação de 2 sublistas, obtém-se uma lista ordenada contendo os elementos das 2 sublistas.
Método Merge Sort
O Merge Sort utiliza a abordagem de "dividir para conquistar". Divide a lista ao meio, ordena as duas sublistas através de chamadas recursivas e então une (Merge) as sublistas ordenadas em uma lista ordenada.
O caso de parada da recursão é quando há apenas um elemento na sublista, estando portanto ordenada.
O algoritmo recursivo é bastante simples, sendo mostrado abaixo:
O procedimento MergeSort utiliza um procedimento chamado Merge que recebe duas listas ordenadas, faz a cópia para uma lista temporária na ordem correta e no final copia os elementos de volta para a lista (antes era dividida em duas sublistas ordenadas).
O Merge Sort tem uma característica importante, que é possuir o mesmo comportamento independente do conteúdo da lista, tendo a mesma complexidade para o melhor, pior ou caso médio.
Tem como desvantagem a necessidade de uma estrutura temporária para efetuar a união (Merge), que deve ter capacidade igual ou superior à da lista a ser ordenada.
Fazendo uma união (Merge) das duas sublistas ordenadas abaixo:
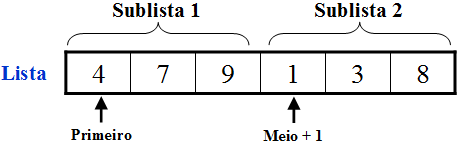
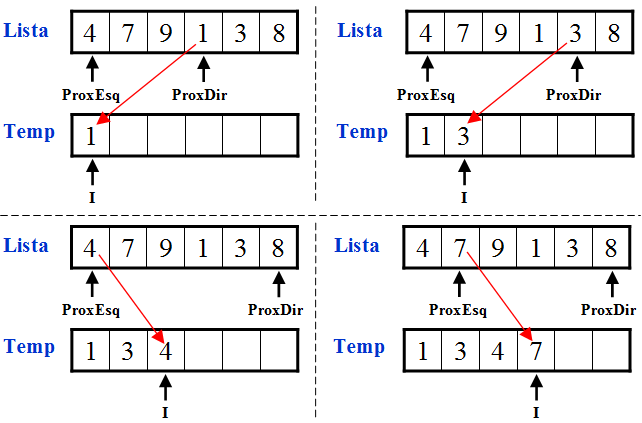
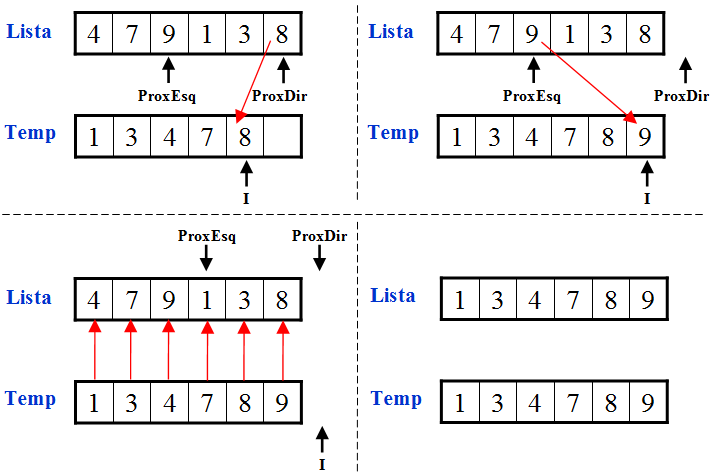
Para ver a implementação do método Merge Sort, abra a unit Intercal.