Árvores Balanceadas AVL

Definição: Uma árvore é considerada AVL quando a altura de suas subárvores direita e esquerda diferem no máximo 1 unidade, isto é, a árvore permanece sempre balanceada. AVL vem da abreviatura dos nomes de seus criadores G.M. Adelson-Velskii e  E.M. Landis, em 1962.

Definição de uma árvore AVL

type
   TDirecao = (NoEsquerdo, NoDireito);
   PNo = ^No;
   No = record
           Dado : Tipo_do_Dado;
           Links : array[NoEsquerdo..NoDireito] of PNo;
           Balanco : -1..1;
   end;
   ArvoreAVL = PNo;

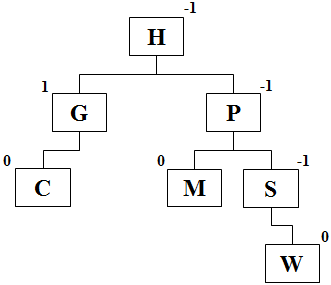
Exemplo: Observe os balanços de cada nó da árvore AVL abaixo

 

Exemplo: Efetuando uma inserção em uma árvore AVL

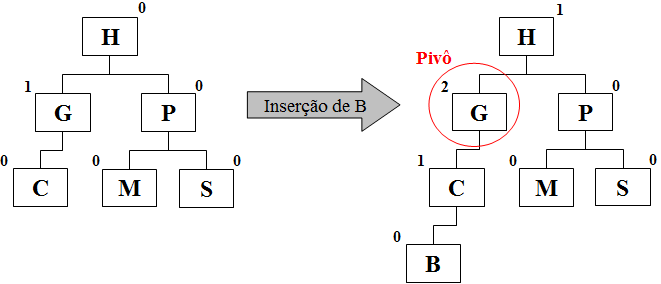
Após a inserção de B no exemplo acima, a árvore passou a ficar desbalanceada. Para corrigir tal situação, aplicamos rotações para tornar a árvore balanceada novamente.

 

Rotações

Rotação Simples para Direita: Quando pivô e filho esquerdo têm mais elementos no lado esquerdo.

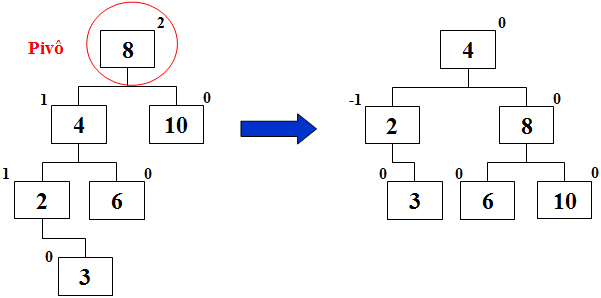
Após a inserção do valor 3, a árvore AVL ficou desbalanceada. O pivô (nó que contém 8) tem balanço 2 e seu filho esquerdo (nó que contém 4) tem balanço 1. Ao aplicar a rotação simples para direita, a árvore volta a ficar balanceada.

 

procedure RotacaoParaDireita(var Pivo : PNo);
var Temp, FilhoEsq : PNo;
begin
   FilhoEsq := Pivo^.Links[NoEsquerdo];
   Temp := FilhoEsq^.Links[NoDireito];
   FilhoEsq^.Links[NoDireito] := Pivo;
   Pivo^.Links[NoEsquerdo] := Temp;
end;

 

Rotação Simples para Esquerda: Quando pivô e filho direito têm mais elementos no lado direito.

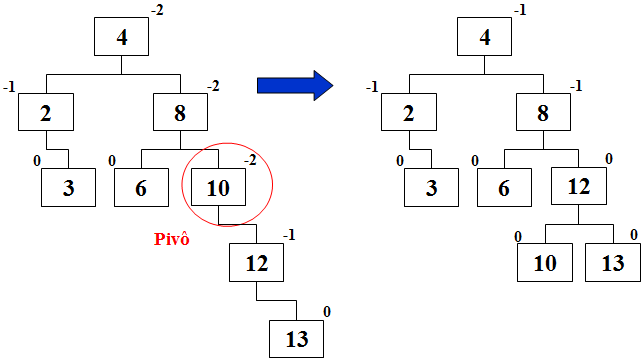
Após a inserção do valor 13, a árvore AVL ficou desbalanceada. O pivô (nó que contém 10) tem balanço -2 e seu filho esquerdo (nó que contém 12) tem balanço -1. Ao aplicar a rotação simples para esquerda, a árvore volta a ficar balanceada.

 

procedure RotacaoParaEsquerda(var Pivo : PNo);
var Temp, FilhoDir : PNo;
begin
   FilhoDir := Pivo^.Links[NoDireito];
   Temp := FilhoDir^.Links[NoEsquerdo];
   FilhoDir^.Links[NoEsquerdo] := Pivo;
   Pivo^.Links[NoDireito] := Temp;
end;

 

Rotação Dupla uma para Esquerda outra para Direita: Quando pivô tem mais elementos do lado esquerdo e filho tem mais elementos do lado direito.

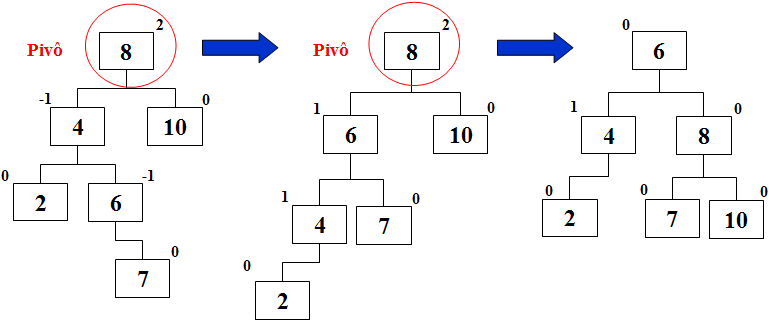
Após a inserção do valor 7, a árvore fica desbalanceada. Como o pivô (nó com valor 8) tem mais elementos do lado esquerdo, mas seu filho esquerdo (nó com valor 4) possui mais elementos do lado direito, é preciso primeiro fazer uma rotação à esquerda em torno do filho esquerdo para depois efetuar a rotação para a direita sobre o pivô.

 

Rotação Dupla uma para Direita outra para Esquerda: Quando pivô tem mais elementos do lado direito e filho tem mais elementos do lado esquerdo.

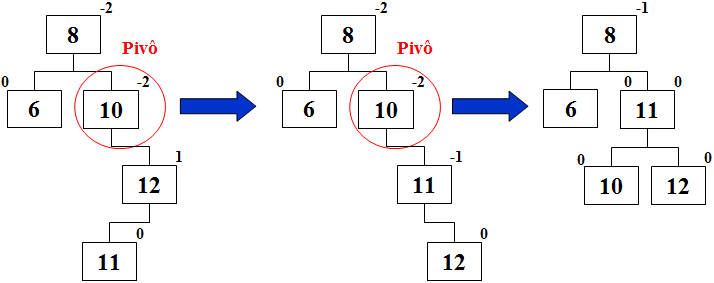
Após a inserção do valor 11, a árvore fica desbalanceada. Como o pivô (nó com valor 10) tem mais elementos do lado direito, mas seu filho direito (nó com valor 12) possui mais elementos do lado esquerdo, é preciso primeiro fazer uma rotação à direita em torno do filho direito para depois efetuar a rotação para a esquerda sobre o pivô (nó com valor 10).

 

De forma geral, teríamos o quadro abaixo:

 

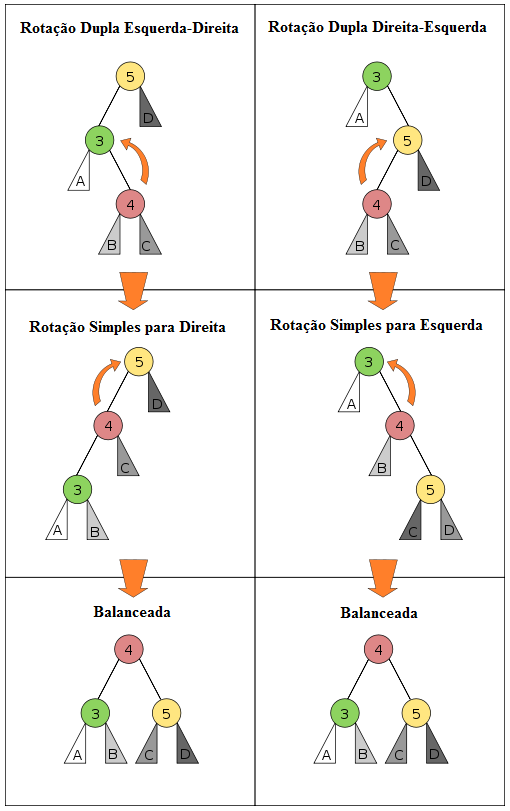
Para ver uma implementação de uma árvore AVL, abra a unit ArvAvl e para um programa que demonstra como usá-la, veja PArvAvl.

A remoção em árvore AVL também pode provocar desbalanceamento, por isso sempre após uma remoção devemos verificar se há necessidade de rotação. A implementação consiste em executar as mesmas rotações acima descritas.